CGAL users discussion list

[Adam Getchell <>]

Hello all,

I was debugging my Pachner move code and ran into the lines:

frame #0: 0x000000010000fd61 unittests`CGAL::Triangulation_data_structure_3<CGAL::Triangulation_vertex_base_with_info_3<unsigned int, CGAL::Epick, CGAL::Triangulation_vertex_base_3<CGAL::Epick, CGAL::Triangulation_ds_vertex_base_3<void> > >, CGAL::Triangulation_cell_base_with_info_3<unsigned int, CGAL::Epick, CGAL::Triangulation_cell_base_3<CGAL::Epick, CGAL::Triangulation_ds_cell_base_3<void> > >, CGAL::Parallel_tag>::is_valid(this=0x0000000100703ea8, verbose=false, level=0) const + 769 at Triangulation_data_structure_3.h:3310

   3307       if ( cell_count - facet_count + edge_count - vertex_count != 0 ) {

   3308         if (verbose)

   3309             std::cerr << "Euler relation unsatisfied" << std::endl;

-> 3310         CGAL_triangulation_assertion(false);

   3311         return false;

   3312       }

   3313

Which is, I believe, enforcing the constraint that the Euler characteristic of the 3D (odd-dimensional manifold) is zero.

Now if I look at the (2,3) Pachner move implemented by flip(Cell_handle, facet) I count as follows:

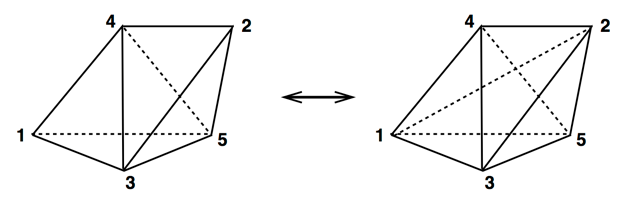
On the left we have:

Cell count: 1345 + 2345 = 2

Facet count: 134 + 135 + 145 + 345 + 234 + 235 + 245 = 7

Edge count: 13 + 14 + 15 + 23 + 24 + 25 + 34 + 35 + 45 = 9

Vertex count: 5

2 - 7 + 9 - 5 = -1 != 0

On the right we have:

Cell count: 1235 + 1234 + 1245 = 3

Facet count: 123 + 125 + 135 + 235 + 124 + 134 + 234 + 145 + 245 = 9

Edge count: 12 + 13 + 14 + 15 + 23 + 24 + 25 + 34 + 35 + 45 = 10

Vertex count: 5

3 - 9 + 10 - 5 = -1 != 0

So, how am I counting wrong? Clearly flip() and flip_really() pass this test.

Looking at the literature[1], they count a triangle in the following manner:

1 2-face (the triangle), 3 1-faces (the edges), 3 0-faces (the vertices), plus the null set = 8. (!)

Any insights appreciated.

[1] http://www.mas.ncl.ac.uk/~nagr1/Colin.pdf

Adam Getchell
about.me/adamgetchell